Sparse nonnegative matrix underapproximation
Starting point to identify major components of combinations of substances using exposure data was to use Non-negative Matrix Factorization (NMF). This algorithm was proposed by Lee and Seung (1999) and Saul and Lee (2002) and deals specifically with non-negative data that have excess zeros such as exposure data. Zetlaoui et al. (2011), introduced this method in food risk assessment to define diet clusters.
The NMF method was then implemented by Béchaux et al. (2013) in order to identify food consumption patterns and main components of combinations of pesticides to which the French population was exposed using TDS exposure to 26 priority pesticides.
At the start of the Euromix project ideas had evolved: to obtain less substances per component experiments were made using Sparse Nonnegative Matrix Factorization (SNMF) (Hoyer (2004)). This method was found not to give stable solutions. Better results were obtained with Sparse Nonnegative Matrix Underapproximation (SNMU) (Gillis and Plemmons (2013)). This model also fits better to the problem situation because also the residual matrix after extracting some components should be nonnegative. The SNMU method has been implemented in MCRA.
Indeed, NMF may be used to identify patterns or associations between substances in exposure data. NMF can be described as a method that finds a description of the data in a lower dimension. There are standard techniques available such as principal components analysis or factor analysis that do the same, but their lower rank representation is less suited because they contain negative values which makes interpretation hard and because of the modelling with a Gaussian random vectors which do not correctly deal with the excess of 0 and non-negative data. The NMF solution approximates a non-negative input matrix (i.c. exposure data) by two constrained non-negative matrices in a lower dimension such that the product of the two is as close as possible to the original input matrix. In Figure 68, the exposure matrix \(M\) with dimensions \(m\) (number of substances) and \(n\) (number of intake days or persons) is approximated by matrix \(U\) and \(V\) with dimensions \((m \times k)\) and \((k \times n)\) respectively, where \(k\) represents the number of components. Matrix \(U\) contains weights of the substances per component, matrix \(V\) contains the coefficients of presence of components in exposure per intake day or person. \(M\) is non-negative (zero or positive) and \(U\) and \(V\) are constraint to be non-negative. The minimization criterion is: \(||M – UV||2\) such that \(U \geq 0\) and \(V \geq 0\).
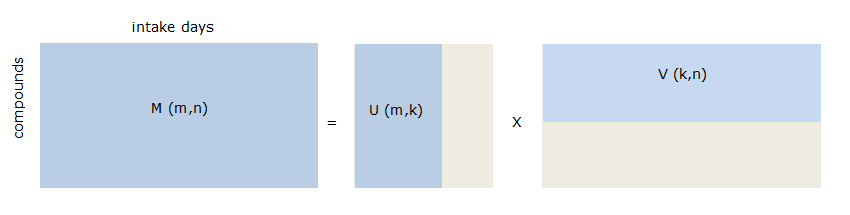
Figure 68 NMF approximation of exposure data
The solution found by NMF contains zeros, but components still contain many substances which complicates interpretability. Therefore, the Sparse Nonnegative Matrix Underapproximation (SNMU) (Gillis and Plemmons (2013)) which also provide sparse results was investigated. The SNMU has also some nice features well adapted to the objective of the Euromix project: the solution is independent of the initialization and the algorithm is recursive. Consequently, the SNMU method which is based on the same decomposition process as the NMF was the one implemented in MCRA.
SNMU is initialized using an optimal nonnegative rank-one approximation using the power method (https://en.wikipedia.org/wiki/Power_iteration). This initialization is based on a singular value decomposition and results in general in a unique solution that is sparse. The SNMU algorithm is called recursive because after identifying the first optimal rank-one underapproximation \(u_{1}v_{1}\), the next rank-one factor is recovered by subtracting \(u_{1}v_{1}\) from \(M\) and applying the same factorization algorithm to the remainder \(M - u_{1}v_{1}\). The solution \(u_{1}v_{1}\) is called a rank-one underapproximation because an upper bound constraint is added to ensure that the remainder \(M - u_{1}v_{1}\) is non-negative. For Matlab code see: https://sites.google.com/site/nicolasgillis/code.
For each component, a percentage of explained variance is calculated. \(M\) is the exposure matrix with \(m\) rows (substances) and \(n\) columns (individuals or individual days) \(S_{t}\) is sum of squared elements of \(M\):
Apply SNMU on \(M\), then for the first component:
\(u\) is \(m \times 1\) vector, contains weights of the component.
\(v\) is \(1 \times n\) vector, contains presence of component in exposure per individual.
Calculate residual matrix \(R\):
\(R = M - uv\)
Calculate \(S_{r}\), residual sum of squared elements of R:
Percentage explained variance first component \((k = 1)\) is:
For the second component:
continue with residual matrix \(R\) (replace \(M\) by \(R\)),
estimate \(u\) and \(v\),
calculate new residual matrix \(R\)
calculate \(S_{r}\), residual sum of squared elements of \(R\)
Percentage explained variance second component \((k=2)\) is:
The last term is de percentage explained variance of the first component. Continue with the third component etc….
The given factorization by SNMU is not unique. A matrix \(D\) and its inverse can be used to transform the two lower rank matrices \(U\) and \(V\) by, e.g.
\(M = UV = UDD^{-1}V\)
where matrix \(D\) is non-negative and corresponds to a scaling of matrix \(U\) and \(V\) to matrix \(\tilde {U} = UD\) and \(\tilde {V} = D^{-1}V\).
In Figure 69, SNMU is applied on the exposure matrix. The SNMU solution after scaling results in a matrix that represents the mixture composition and a matrix representing the individual scores. The first matrix is interpreted as the set of contributions of the substances to a component., the second matrix, as the set of exposures of the individuals to the mixtures.
Figure 69 SNMU approximation of exposure data after scaling.
Exposure matrix
Basically, exposure is calculated as consumption x concentration. By summing the exposures from the different foods for each substance per person day separately, the exposure matrix for component selection is estimated:
where \(y_{ijc}\) is the exposure to substance \(c\) by individual \(i\) on day \(j\) (in microgram substance per kg body weight), \(x_{ijk}\) is the consumption by individual \(i\) on day \(j\) of food \(k\) (in g), \(c_{ijkc}\) is the concentration of substance \(c\) in food \(k\) eaten by individual \(i\) on day \(j\) (in mg/kg), and \(\mathit{bw}_{i}\) is the body weight of individual \(i\) (in kg). Finally, \(p\) is the number of foods accounted for in the model. More precisely, for an acute or short term risk assessment, the exposure matrix summarises the \(y_{ijc}\) with columns denoting the individual-days \((ij)\) and rows denoting the substances \((c)\). Each cell represents the sum of the exposures for a substance on that particular day. For a chronic or long term risk assessment, the exposure matrix is constructed as the sum of all exposures for a particular substance averaged over the total number of intake days of an individual (substances x persons). So each row represents a substance and a column an individual. Each cell represents the observed individual mean exposure for a substance for that individual. Note that in the exposure calculation, the concentration is the average of all residue values of a substance.
When relative potency factors (RPF) are available then exposures are multiplied by the RPF and thus exposures to the different substances are on the same and comparable scale (toxicological scale). In this case, the selection of the components is risk-based. In some cases, RPFs may not be available. In this case exposure to different substances, even in the same unit, may lead to very different effects. To give all substances an equal weight a priori and avoid scaling effects, a standardisation of the data can be applied as done in Béchaux et al. (2013). In this case, all substances are assigned equal mean and variance, and the selection of the components will work on patterns of correlation only. Then component selection is not risk-based anymore but, what could be called, co-exposure-based.
Finally, in the mixture selection module of MCRA, the SNMU expects RPF data for a risk-based selection. If not available, the user should provide alternative RPF data, e.g. values 1 for a purely exposure-based selection, or lower-tier estimates (e.g. a maximum value on RPF thought possible).
Mechanisms to influence sparsity
Two mechanisms to influence sparsity are available. The SNMU algorithm incorporates a sparsity parameter and by increasing the value, the final components will be more sparse (sparsity close to 0: not sparse, many substances; sparsity close to 1: sparse, few substances). The other approach is by using a subset of the exposure matrix based on a cut-off value for the MCR. High ratios correspond to high co-exposure, so it is reasonable to focus on these (person) days and not include days where exposure is received from a single substance (ratio close to 1). To illustrate the combined use of MCR and the sparsity parameter, the French steatosis data (39 substances, 4079 persons) are used and person days with a ratio > 5 (see Figure 63) are selected yielding a subset of 139 records.
In Figure 70, the effect of using a cut-off level is immediately clear. The number of substances of the first component is 17 whereas in the unselected case (not shown) only 4 substances were found The three plots show the influence of increasing the sparsity parameter from 0 to 1 on the number of substances in the component. The first plot shows the estimated sparsity versus the specified sparsity. The second and third plot the the numer of substances in a component. For values close to 0, the component contains 17 substances. For values > 0.4 the number of substances in the component drops to 3 and for a sparsity close to 1, only one substance is found in a component.
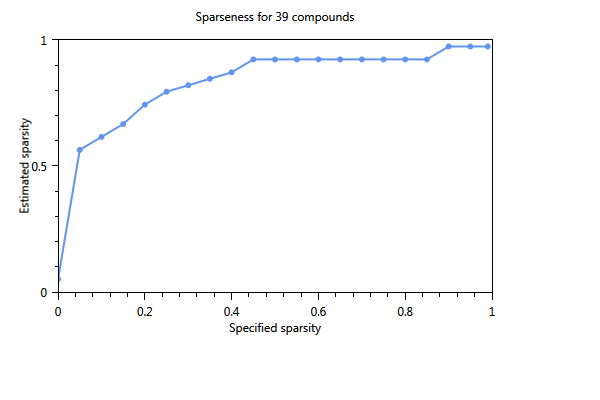
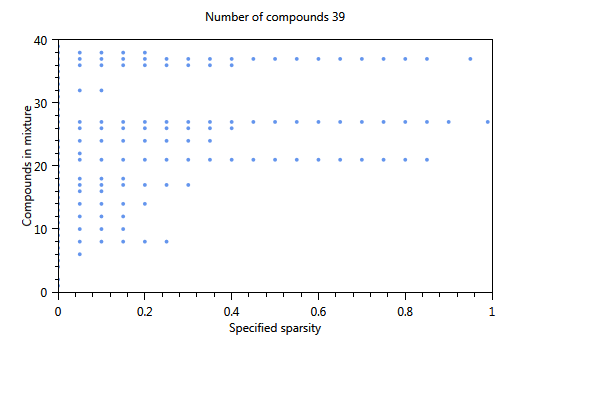
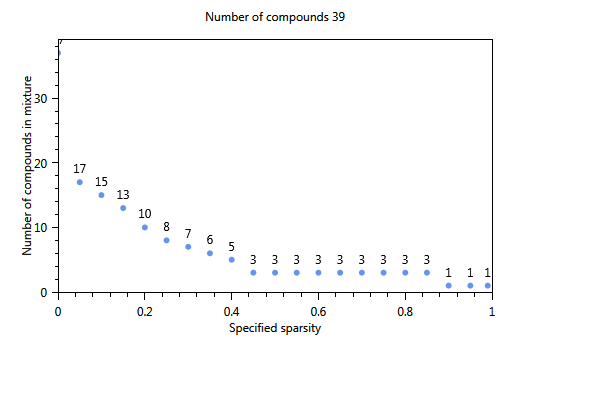
Figure 70 Influence of the specified sparsity parameter on the realized sparsity, n = 139.